Definicija:
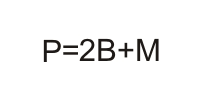

Površina valjka
Valjak ili cilindar (od grčke reči kýlindros — kotrljati, valjati) je konveksno geometrijsko telo. Može se definisati pomoću jedne elipse i duži u prostoru. Ukoliko se jedno teme date duži postavi u centar date elipsea elipsa neprekidno umnožava duž nje, dobijeno telo će biti upravo valjak. Pri tom su radijusi ove elipse takođe radijusi valjka, dužina date duži je dužina izvodnice valjka, a rastojanje između ravni kojima pripadaju dve najudaljenije elipse visina valjka. Prava kojoj pripada data duž se naziva osa valjka. Elipsa od koje je razvoj tela krenuo se naziva baza valjka. Površkoja ograničava valjak, kada mu se oduzmu dve elipse sa centrima u temenima date duži, se zove omotač valjka.

Ukoliko je osa valjka normalna na bazu valjka, telo se zove pravi valjak, kod koga su dužine izvodnice i visine jednake. U suprotnom se radi o kosom valjku, čija je izvodnica uvek duža od visine. Zavisno od toga da li je baza prava elipsa ili krug, valjak se zove eliptični, odnosno kružni valjak.
1.Pravi valjak 2.Kosi valjak
Površina valjka
Površina kružnog jednakostraničnog valjka (P) je odredjena kao zbir površine omotača valjka i dupla površina njegove baze. Površina omotača se računa kao proizvod dužina obima baze i izvodnice valjka. Formula za izračunavanje površine valjka je sledeća:
Objašnenje za obrazac- P(B) predstavlja površinu baze, a P(M) površinu omotača valjka. Površina omotača je već opisana kao:
Potrebno je voditi računa da kod pravog valjka važi pravilo da je h=l. Kod kosog valjka izvodnica ne mora uvek biti data eksplicitno. Možemo je izračuati uz omoć dužine visine (h) i jednog ugla. To je obično ugao između baze i ose valjka, ili njegov komplement, odnosno ugao između normale na bazu i ose valjka. Tako se mogu dobiti dve naredne formule:
Zapremina valjka
Zapremina valjka (V) se dobija kao proizvod površine bazne elipse i visine valjka. Njena formula bi tako bila sledeća:
Ovde B predstavlja površinu baze, a h visinu valjka. I ovde važi da, ako visina valjka nije data eksplicitno, ona se može odrediti pomoću dužine izvodnice i jednog ugla, kao što je to opisano u pretodnom primeru.






Нема коментара:
Постави коментар